
In the current version of Eurocode 5 (EN 1995-1-1:2004+A2:2014) you can find equations that relate to the lateral torsional buckling of beams.
Equation 6.31 gives the critical bending stress
Where:
E0,05 is the fifth percentile value of modulus of elasticity parallel to grain
G0,05 is the fifth percentile value of modulus of elasticity parallel to grain
Iz is the second moment of area about the weak axis
Itor is the torsional moment of inertia
lef is the effective length of the beam (depending on support conditions and loading configuration)
Wy is the section modulus about the strong axis
For graded timber, you can find a value of fifth percentile value of modulus of elasticity parallel to grain (E0,05) by looking at the strength class table in EN338 (or the equations for secondary properties (which have been moved to the 2016 version of EN384). But you won’t find a value for fifth percentile value of modulus of elasticity parallel to grain. So what do you do?
Well, if you have rectangular cross-section softwood you have a solution in the form of equation 6.32:
So what value of G0,05 does this equation imply? We might use the EN338/EN384 calculation of Gmean from Emean and make an educated guess that G0,05 = E0,05 / 16
Does this guess check out? The answer is interesting: it depends.
We have a rectangular cross-section in which:
b = the width of the beam (smaller cross-section dimension)
h = the depth of the beam (larger cross-section dimension)
Iz = bh3/12
Wy = bh2/6
Itor = Βhb3 in which Β is a constant that depends on the aspect ratio of the cross-section
If we set that G0,05 = E0,05 / A
And rearrange and simply Equation 6.31 = Equation 6.32
We end up with
A = 48.7B
The value of B for a cross-section of infinite aspect ratio is 1/3 so our guess that A is 16 checks out at that end of the scale
But for non-infinite aspect ratios we have a rather strange situation – the ratio of G and E assumed varies, depending on the ratio of b and h.
| h/b | B (a textbook value) | A (which is E0,05 / G0,05) |
| 1 | 0.141 | 6.8 |
| 1.5 | 0.196 | 9.5 |
| 2 | 0.229 | 11.1 |
| 2.5 | 0.249 | 12.1 |
| 3 | 0.263 | 12.8 |
| 4 | 0.281 | 13.7 |
| 5 | 0.291 | 14.2 |
| 6 | 0.299 | 14.6 |
| 10 | 0.312 | 15.2 |
| Infinity | 0.333 | 16.2 |
Now, we know that E and G are not well correlated for pieces within a species (e.g. ref) so actually it is not so likely that a piece will, simultaneously, have both low E and low G. Lateral torsional buckling is also less critical for the smaller aspect ratios …and so perhaps it is reasonable that we have an equation that gets closer to the more conservative value as buckling becomes more of an issue.
This leaves an open question – what value of 5th percentile shear modulus should you take for hardwoods? EN338/EN384 imply the same ratio G0,05 = E0,05 / 16 for hardwoods so why is equation 6.32 specifically limited to softwoods? Not sure – perhaps it is thought that the lower amount of knowledge we have of hardwood properties means that you should not be allowed that extra headroom for the beams with lower aspect ratios.
In summary – it is not very helpful that EN1995 requires you to use a property that is not listed among the strength class values.
By the way, for softwood glulam, EN14080:2013 gives a conversion in clause 5.1.3
Gg,k/Gg,mean = 5/6
Since, for softwood, EN338/EN384 tells us that E0,05 is 2/3 * Emean and Gmean is Emean/16 this is equivalent to
G0,05 = Gmean * 5/6 = Emean/16 * 5/6 = 3/2 * E0,05/16 * 5/6
G0,05 = E0,05/12.8
E0,05 = 2/3 * Emean is equivalent to an assumption that E is normally distributed with a coefficient of variation of about 20%
G0,05 = 5/6 * Gmean is equivalent to an assumption that G is normally distributed with a coefficient of variation of about 10%

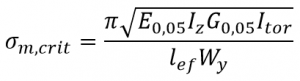
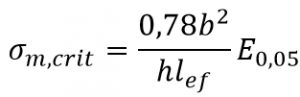
Leave a Reply
You must be logged in to post a comment.