
The 2016 version of EN338 brought a few changes. One of these changes was the addition of a table of tension strength classes (T classes).
Tension strength classes are intended for use in making glulam – and they have been in use for quite a long time already. The inclusion in EN338 is intended to simplify matters across all timber related standards.
Grading is based on three primary properties: strength, stiffness and density. For C and D strength classes the key strength is the major axis bending strength. Since you can only destructively test timber in one way, the other properties have to be conservatively estimated from the three properties we measure when we establish the grading rules (see EN384:2016 Table 2).
So, for C and D classes, tension strength is a secondary property, conservatively estimated from bending strength. (The same is true of shear strength and compression strength parallel to grain).
The difference between tension grades and bending grades is that tension grades are established based on the results of tension tests, rather than bending tests. That means that bending strength for the strength class is estimated from tension strength rather than the other way around. This explains why, if you compare the values for C and T grades you will see that tension strength is better for T grades.
So, for T classes bending strength is a secondary property, conservatively estimated from tension strength. (The same is true of shear strength and compression strength parallel to grain).
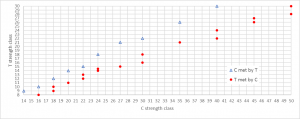
The consequence of this is that there is no simple one-to-one correspondence between C and T classes. You can say that the requirements of a T class can be met by a certain C class – but this equivalence does not work in the other direction. You can find the first kind of correspondence (T met by C) in Table 1 of EN14080:2013 but be aware that this is not correct to the 2016 version of EN338 for classes T12 and below because this revision also changed the tension strengths of the bending classes (based on Gradewood test data). Table 1 of EN14080:2013 has a footnote with dated reference to EN338:2009.
You can work out the correspondence of C and T classes by comparing all property values in the most recent version of EN338. At time of writing, this is EN338:2016 and the correspondence is as follows:
T classes can be met by C classes
T8 by C16
T9 by C18
T10 by C18
T11 by C20
T12 by C22
T13 by C22
T14 by C24
T14.5 by C24
T15 by C27
T16 by C30
T18 by C30
T21 by C35
T22 by C40
T24 by C40
T26 by C45
T27 by C45
T28 by C50
T30 by C50
C classes can be met by T classes
C14 by T9
C16 by T10
C18 by T12
C20 by T14
C22 by T15
C24 by T18
C27 by T21
C30 by T22
C35 by T26
C40 by T30
C45 (not possible)
C50 (not possible)
The difference in direction is quite big at the high end. T24 can be met with C40, but T24 is only sufficient to meet C30. C40 requires T30.

Another reason there is no simple correspondence between C and T classes is the MOE: The MOE for C classes is defined in bending, the MOE for T classes is defined in tension. Therefore, in EN 338 are used different symbols: Em,0,mean/Em,0,k (for C classes) and Et,0,mean/Et,0,k(for T classes). Only when assuming they are of the same magnitude the correspondence becomes easy.
Yes, this is true! Although using EN1995 involves this assumption too.
The Gradewood project report (e.g. Figure 28 on page 47) gives us some confidence that this is a reasonable assumption to make.
https://www.vtt.fi/inf/pdf/workingpapers/2011/W179.pdf