
We all know that Santa is going to find out whether a child has been naughty or nice – but how does he do it? Back in 2016 I wrote about it on this blog, but I think it needs an update. Let’s recap some key points:
- We know naughty and nice are binary states for Santa’s decision (Gillespie & Coots, 1934). A child either gets a stocking filled with presents or gets coal.
- We also know that actual naughtiness and niceness are analogue. A child can be a bit naughty or very naughty; a bit nice or very nice.
- We can think of this as being a scale with naughty towards one end and nice towards the other.
- A child’s naughtiness level varies over time, so they’ll move along the scale over time, depending on their moods and opportunities.
- Over the course of the year, each child will accumulate a distribution of naughtiness and niceness – spending a certain amount of time at different naughtiness levels.
- But we don’t really know the shape of this distribution.
The original question back in 2016 was “how does Santa turn this this distribution of naughtiness and niceness into a binary decision and classify each child as being either naughty or nice?”
I discussed the idea that even if Santa had perfect knowledge (which, of course he might) his decision is probably not best made on a simple average, but instead to focus on something about the naughtiest end – how long being beyond a certain level of naughty – or what level of naughty was achieved. So far, so sensible.
But then I discussed what Santa might do if he didn’t have perfect knowledge and instead had to rely on some occasional measurements. How could he do it then? This brought up two risks for Santa to consider (even if he checks his list twice):
- Child’s risk: a child is declared naughty when they are actually nice (Type I error – “incorrectly naughty”)
- Santa’s risk: a child is declared nice when they are actually naughty (Type II error – “incorrectly nice”)
Somehow, those two risks need to be balanced, and Santa has to make a decision about how acceptable he finds them. He probably considers reducing the child’s risk to be more critical than reducing his risk since he is notoriously jolly.
Let’s look a bit more into that, but lay out a simplified example. We will assume that:
- Santa makes observations of a whole day.
- The number of days on which to make observations can be varied.
- Assessment is made over one year (from Christmas day to Christmas day).
- Santa’s observation days are chosen randomly.
- There is no structure to the naughtiness distribution over the year – it is purely random.
- Santa decides how many days to observe before making any observations.
- Santa’s observations do not affect the child’s behaviour.
2024 was a leap year with 366 days, which means Santa could observe all 366 days, rank each day by naughtiness and make his judgement on the basis of the naughtiest day. But what if Santa only observes some days? Well, if he did not observe all, there is a possibility he did not observe the naughtiest day. If he observed 365 days he might have only seen the second naughtiest day. If he observed 364 the third naughtiest … and so on.
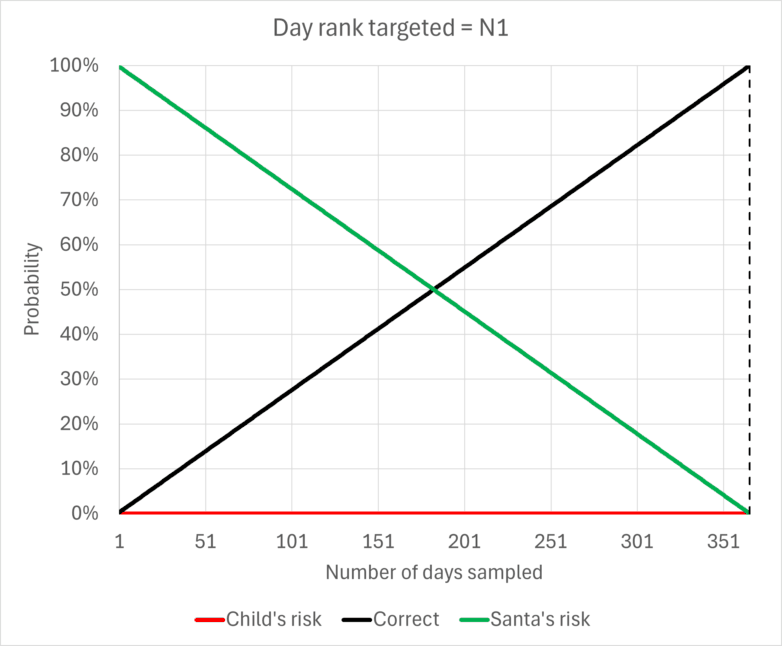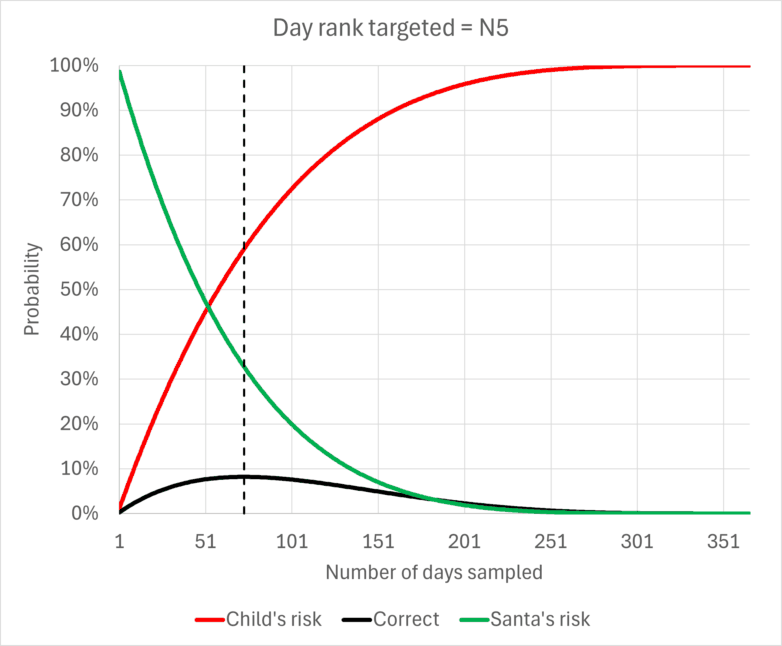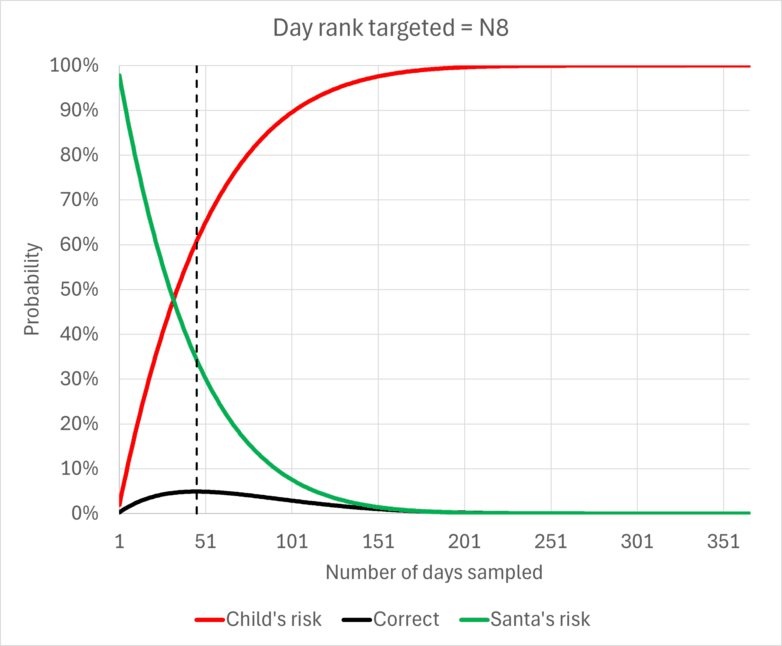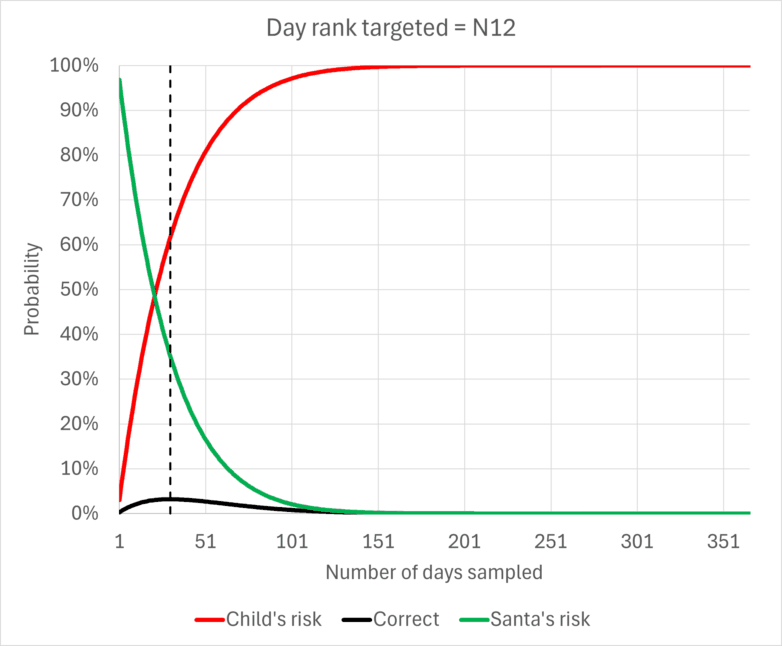
To make this easier to talk about, we can think about the 366 days ranked in order from naughtiest to nicest: N1, N2, N3, N4… N364, N365, N366. The naughtiest day is N1.
We can calculate the probability of Santa randomly not observing N1 like we calculate the probability of balls drawn from a bag without replacement (or, if you prefer, a sack of numbered sprouts). If Santa observes one day, the probability of not observing N1 is 365/366. This is the same probability for any of the other days we might select as the rank of interest.
For any number of days sampled we can calculate using the pattern:
365/366 * (365-1)/(366-1) * (365-2)/(366-2) * (365-3)/(366-3) * (365-4)/(366-4)…
…using as many terms as there are days sampled. Lets call this probability of not observing a particular day P, for a certain number of sampled days. The equation for P simplifies:
P = (366 – number of sampled days) / 366
If Santa observes 183 days it is quite likely he does not see N1. P(183) is 50%. So Santa might instead assume that the worst he sees is N2. However, this carries the risk that the worst he sees is actually N3 or higher. In that case he would be underestimating naughtiness. That would be related to “Santa’s risk”. But there is also the possibility that he did see N1, and therefore overestimated naughtiness in thinking there was a naughtier day than that. This would be related to the “child’s risk”. It is not necessarily the case that Santa thinking N3 is N2 results in a naughty child being declared nice, or that Santa thinking N1 is N2 results in a nice child being declared naughty. It also depends on Santa’s naughtiness threshold, and how naughty N1 and N3 are for a particular child. But we do not know these things, so for shorthand let’s call them “child’s risk” and “Santa’s risk” anyway.
The child’s risk is the possibility of observing N1, which is 1-P.
Santa’s risk is the possibility of not observing N1 nor N2, which is P * P.
The other possibility is getting the assessment right – observing N2, but not N1. This is P * (1-P).
In the case of 183 sampled days, assessing N2, the child’s risk would be 50% and Santa’s risk would be 25%. The probability of the assessment being spot on is 25%.
Edit 03/01/2025: What follows is an approximation that avoids the need for calculating factorials. This approximation works well enough because 366 is a relatively large number to be sampling from, and we are only interested in the lowest ranks. The proper formulas are given at the bottom of the page.
We can extend this to any particular day rank. For Nn the formulas are:
The child’s risk = 1 – P^(n-1)
The probability a day below rank n is observed
=1 – the probability no day below rank n is observed.
Santa’s risk = P^n
The probability no day below and including rank n is observed.
Correct assessment = (1-P) * P^(n-1)
The probability no day below rank n is observed, but day rank n is.
These allow calculations for various numbers of days sampled and ranks considered. For example, if targeting N2, Santa could balance his and the child’s risk by surveying 140 days rather than 183. This comes with the additional advantage of also being less effort for Santa. But the child’s risk is almost always rather high… what is acceptable? 1 in 20 children having their naughtiness overestimated? A child’s risk level of even 5% seems high. How can it be avoided?
Well, there is one way. Santa can assume the worst day he sees is N1. That way, there is no child’s risk. The worst that can happen is that a child is correctly assessed. Then Santa can pick how many days to assess, based only on his own level of acceptable risk – content in the knowledge that no nice child will be declared naughty. Santa’s risk is children who are occasionally naughty still getting presents – something we might have some direct evidence of from our own childhoods.
This is the case if Santa assumes the worst day he sees is the target day. Of course he might not do it that way. He might use instead the second worst day he sees – or the third. Or some combination. We might also think about the possibility of Santa takings instantaneous measurements rather than a whole day – which is like sampling from a bag of infinitely many balls. This could be modelled with the binomial distribution. The mathematics is left as a Christmas exercise for the reader – but here is a clue.
Does this change the original conclusion from 2016? A bit, but not a lot. It is still the case that “Be good for goodness sake” is not the best advice. Better to consolidate all your naughtiness into certain periods of time in order to defeat Santa’s naughtiness sampling protocol.
Reference:
Coots, J.F. & Gillespie, H., “Santa Claus Is Coming to Town”, Decca, 1934
Edit 03/01/2025: To do a proper calculation we need to fully account for the effects of “drawing without replacement”. Above we assumed that the probability P does not change once we have already drawn, but in fact it does. A fully correct calculation involves calculating factorials – which gets pretty difficult for large numbers.
The number of possible combinations of r randomly chosen from n = combin(n, r) = n! / (r! * (n-r)! )
For s sampled days, we already have
P = (366 – s) / 366
The child’s risk = 1 – combin(N-n+1,s) / combin(N,s)
The probability a day below rank n is observed.
Santa’s risk = combin(N-n,s) / combin(N,s)
The probability no day below and including rank n is observed.
Correct assessment = (1-P) * combin(N-n,s-1)/combin(N-1,s-1)
The probability no day below rank n is observed, but day rank n is.

Leave a Reply
You must be logged in to post a comment.